This lecture is the intellectual property of Professor S.W. Hawking. You may not reproduce, edit or distribute this document in anyway for monetary advantage.
In science fiction, space and time warps are a commonplace. They are used for rapid journeys around the galaxy, or for travel through time. But today's science fiction, is often tomorrow's science fact. So what are the chances for space and time warps.
The idea that space and time can be curved, or warped, is fairly recent. For more than two thousand years, the axioms of Euclidean geometry, were considered to be self evident.
 As
those of you that were forced to learn Euclidean geometry at school may
remember, one of the consequences of these axioms is, that the angles
of a triangle, add up to a hundred and 80 degrees.
As
those of you that were forced to learn Euclidean geometry at school may
remember, one of the consequences of these axioms is, that the angles
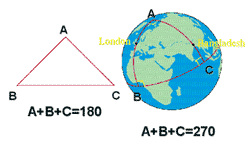
of a triangle, add up to a hundred and 80 degrees. However, in the last century, people began to realize that other forms of geometry were possible, in which the angles of a triangle, need not add up to a hundred and 80 degrees. Consider, for example, the surface of the Earth. The nearest thing to a straight line on the surface of the Earth, is what is called, a great circle. These are the shortest paths between two points, so they are the roots that air lines use. Consider now the triangle on the surface of the Earth, made up of the equator, the line of 0 degrees longitude through London, and the line of 90 degrees longtitude east, through Bangladesh.
 The
two lines of longitude, meet the equator at a right angle, 90 degrees.
The two lines of longitude also meet each other at the north pole, at a
right angle, or 90 degrees. Thus one has a triangle with three right
angles. The angles of this triangle add up to two hundred and seventy
degrees. This is greater than the hundred and eighty degrees, for a
triangle on a flat surface. If one drew a triangle on a saddle shaped
surface, one would find that the angles added up to less than a hundred
and eighty degrees. The surface of the Earth, is what is called a two
dimensional space. That is, you can move on the surface of the Earth,
in two directions at right angles to each other: you can move north
south, or east west. But of course, there is a third direction at right
angles to these two, and that is up or down. That is to say, the
surface of the Earth exists in three-dimensional space. The three
dimensional space is flat. That is to say, it obeys Euclidean geometry.
The angles of a triangle, add up to a hundred and eighty degrees.
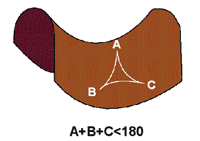
However, one could imagine a race of two dimensional creatures, who
could move about on the surface of the Earth, but who couldn't
experience the third direction, of up or down. They wouldn't know about
the flat three-dimensional space, in which the surface of the Earth
lives. For them, space would be curved, and geometry would be
non-Euclidean.
The
two lines of longitude, meet the equator at a right angle, 90 degrees.
The two lines of longitude also meet each other at the north pole, at a
right angle, or 90 degrees. Thus one has a triangle with three right
angles. The angles of this triangle add up to two hundred and seventy
degrees. This is greater than the hundred and eighty degrees, for a
triangle on a flat surface. If one drew a triangle on a saddle shaped
surface, one would find that the angles added up to less than a hundred
and eighty degrees. The surface of the Earth, is what is called a two
dimensional space. That is, you can move on the surface of the Earth,
in two directions at right angles to each other: you can move north
south, or east west. But of course, there is a third direction at right
angles to these two, and that is up or down. That is to say, the
surface of the Earth exists in three-dimensional space. The three
dimensional space is flat. That is to say, it obeys Euclidean geometry.
The angles of a triangle, add up to a hundred and eighty degrees.
However, one could imagine a race of two dimensional creatures, who
could move about on the surface of the Earth, but who couldn't
experience the third direction, of up or down. They wouldn't know about
the flat three-dimensional space, in which the surface of the Earth
lives. For them, space would be curved, and geometry would be
non-Euclidean. It would be very difficult to design a living being that could exist in only two dimensions.
Food that the creature couldn't digest would have to be spat out the same
 way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart.
way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart.
So three dimensions, seems to be the minimum for life. But just as one can think of two dimensional beings living on the surface of the Earth, so one could imagine that the three dimensional space in which we live, was the surface of a sphere, in another dimension that we don't see. If the sphere were very large, space would be nearly flat, and Euclidean geometry would be a very good approximation over small distances. But we would notice that Euclidean geometry broke down, over large distances. As an illustration of this, imagine a team of painters, adding paint to the surface of a large ball.
 As the thickness of the paint layer increased, the surface area would
go up. If the ball were in a flat three-dimensional space, one could go
on adding paint indefinitely, and the ball would get bigger and bigger.
However, if the three-dimensional space, were really the surface of a
sphere in another dimension, its volume would be large but finite. As
one added more layers of paint, the ball would eventually fill half the
space. After that, the painters would find that they were trapped in a
region of ever decreasing size, and almost the whole of space, was
occupied by the ball, and its layers of paint. So they would know that
they were living in a curved space, and not a flat one.
As the thickness of the paint layer increased, the surface area would
go up. If the ball were in a flat three-dimensional space, one could go
on adding paint indefinitely, and the ball would get bigger and bigger.
However, if the three-dimensional space, were really the surface of a
sphere in another dimension, its volume would be large but finite. As
one added more layers of paint, the ball would eventually fill half the
space. After that, the painters would find that they were trapped in a
region of ever decreasing size, and almost the whole of space, was
occupied by the ball, and its layers of paint. So they would know that
they were living in a curved space, and not a flat one.This example shows that one can not deduce the geometry of the world from first principles, as the ancient Greeks thought. Instead, one has to measure the space we live in, and find out its geometry by experiment. However, although a way to describe curved spaces, was developed by the German, George Friedrich Riemann, in 1854, it remained just a piece of mathematics for sixty years. It could describe curved spaces that existed in the abstract, but there seemed no reason why the physical space we lived in, should be curved. This came only in 1915, when Einstein put forward the General Theory of Relativity.