Following a suggestion by NAS member Lloyd Berkner, the International Council of Scientific Unions (ICSU) in 1952 proposed a comprehensive series of global geophysical activities to span the period July 1957-December 1958. The International Geophysical Year (IGY), as it was called, was timed to coincide with the high point of the eleven-year cycle of sunspot activity.

In March of 1953, the NAS appointed a US National Committee to oversee US participation in the IGY. The US program included investigations of aurora and airglow, cosmic rays, geomagnetism, glaciology, gravity, the ionosphere, determinations of longitude and latitude, meteorology, oceanography, seismology, solar activity, and the upper atmosphere. In connection with upper atmosphere research, the US undertook to develop an orbiting satellite program. It was from the IGY rocket and satellite research that the US developed its space program -- with the advice of the NAS Space Science Board.

The International Geophysical Year collection contains correspondence, reports, meeting minutes, photographs, and other records documenting the programs and activities of the US National Committee for the IGY. The collection covers the years 1953-1962 and spans approximately 152 linear feet. The historical records of the IGY can be found in the Archives of the National Academy of Sciences-National Research Council; e-mail archives@nas.edu for further information. 

Text copied by permission of the National Academy of Sciences.

http://history.nasa.gov/sputnik/igy.html

US Announcement 

President Eisenhower's Science Advisory Committee had earlier recommended that a U.S. earth satellite program as a contribution to the International Geophysical Year (IGY) was warranted because of its scientific merit, and especially because it would test "Freedom of Space" as a principle of international law. The U.S. IGY Satellite Program, later called "Vanguard," was approved by the President. James Hagerty, Presidential Press Secretary, called a closed press conference on July 28, 1955, which was followed by a press announcement the next morning, and a press conference with TV and radio coverage that afternoon. Hagerty's statement of July 29 ran as follows:

    On behalf of the President, I am now announcing that the President has approved plans by this country for going ahead with the launching of small earth-circling satellites as part of the United States participation in the International Geophysical Year... This program will for the first time in history enable scientists throughout the world to make sustained observations in the regions beyond the earth's atmosphere.

    The President expressed personal gratification that the American program will provide scientists of all nations this important and unique opportunity for the advancement of science.

President Eisenhower later explained further in his memoirs, as follows:

    In the United States we were careful to keep the earth satellite program separated from the Defense Department's work on long-range ballistic missiles. Though the Navy would supply the launching facilities for the satellite, it was to go into orbit strictly as a peaceful scientific experiment, and was not to interfere with our top priority work on missiles. No secret missile information would be involved in the satellite program; our scientists deliberately planned to share all information acquired with participating scientists all over the world.

SOURCE:  History at NASA

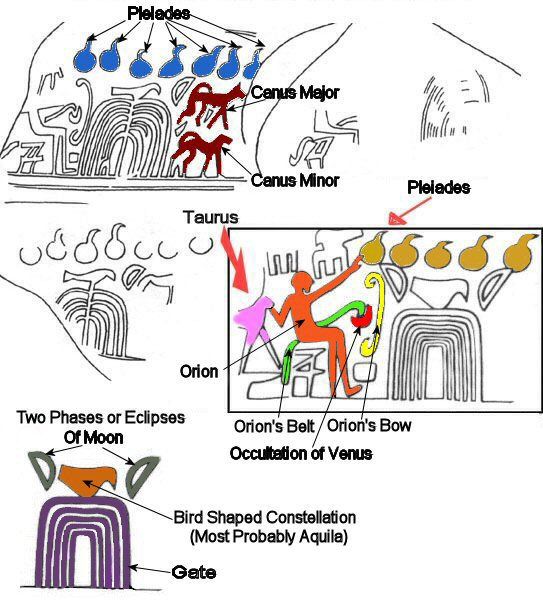
Originally posted by starwarp2000
reply to post by undo

UPDATE ON POSSIBLE STAR MAP DEPICTED IN DRAWING

Hi undo,
After much research into the most significant Constellations of the Era, and the depictions represented on the artifact, I have come to this preliminary conclusion:

1. The Seven Orbs (onions) are definitely The Pleiades.
2. The Two Dog shapes are definitely Canus Major and Canus Minor.
3. The Bull is Taurus.
4. Orion's Body, Belt and Bow are depicted correctly.
5. Orion's belt is occulting Venus.

The Gate

Above the gate is a bird shape, and this could be Cygnus or Aquila. After consultation with the Almanacs and the figures depicted in the two pictures above left in the original, it most definitely has to be 'Aquila' as it depicts an Eagle not a Swan.
It seems to be stating that there are two phases or partial eclipses of the moon equidistant and on alternate sides of Aquila.
I still have to determine when this occurred, but my preliminary date places it in or about 10,500 BC.

Will keep you updated when I ascertain any new information.

Cheers
 
Related Links:

• Francesco Raffaelle - Late Predynastic and Early Dynastic Egypt - Horus NARMER (from the Main Deposit Palette) Click on this image to go to the PALETTES CORPUS 
• History and Archaeology of the Egyptian Early Dynastic Period
• This is a detailed account of the History and Archaeology of the Egyptian Early Dynastic Period: check out the pages on the Second and Third Dynasty and on Dynasty 0. If you are interested in Late Predynastic Egypt (Protodynastic) and Early Dynastic period you'll certainly find here what you're searching for. There are also 4 corpora: First Dynasty Wooden and Ivory Labels, Early Dynastic Inscriptions on Stone Vessels, Naqada IIIb1-2 serekhs and Late Predynastic Decorated Palettes; articles, news, many pictures, images galleries, links and especially abundant text. Nice reading Francesco Raffaele
• On the terms "Dynasty 0" and "Dynasty 00" * - (Francesco Raffaele, Jan. 2003) 

• Amazing Pyramid "Facts"
• THE ROSICRUCIANS THEIR RITES AND MYSTERIES
• Dendera Zodiacs
• Dendera Temple Crypt
• Translation of the figures in the Zodiac of Denderah
  

Observations of planets “travel backwards”

The very existence of the precise planetary positions on the Senmut star map, and on other star maps of that era c. 1500-1300 BC, demonstrates an expertise concerning the calculations of planetary positions. The fact that these maps include such details as a retrograde planet - Mars - and a solar eclipse position (proven to be exactly as stated on the Senmut map), exclude any possibility of coincidence.

A thousand years before the time of Senmut, the astronomer-priests were developing such skills by constant observation of the firmament, which necessitated the keeping of accurate records, especially with regard to calculating celestial positions and cyclic phenomena. The data were used for the sun- and star-related calendars as well as the “star clock”. Records of such astronomical calculations, however, do not seem to have survived, although there are examples of very ancient calendars. But as documented by e.g. inscriptions - a planet “...travels backwards...” - a retrograde movement of a planet placed opposite to the sun was a well-known phenomenon.

The precise positioning of planets by observing them, even in bright daylight, from the bottom of deep wells or shafts directly (and probably less by oblique mirror-reflection in a water surface in the well), was a widely known practice in all ancient cultures.

Furthermore, one of the oldest known Egyptian presentations of a planetary position, places Jupiter close to the decan (celestial sector of 10-degrees) of Sirius. This dates back some 4200 years, and is recorded on a fragment of a starclock-diagram depicted inside a coffin-lid (on Heny's coffin) - one of the traditional methods of recording.

http://www.ovs.thirax.dk/Artikel-X/Ove21/index-uk.htm

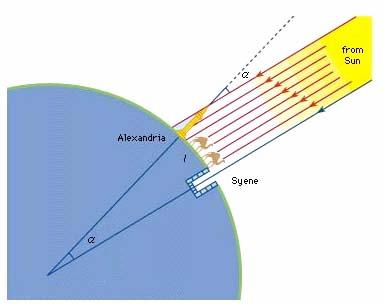
It has been doubted - under the modern time's drawback of historical knowledge - and has been called “a myth”, that astronomers of ancient times used wells/shafts at all, in order to make observations from them. Plato (428-348 BC) mentions that the philosopher Thales of Miletus (c. 640-547 BC) had an accident in a well while observing the stars. - And the Greek author Aesop (6th c. BC) tells similarly concerning another astronomer in a well-shaft.

An ancient apocryphal text, c. 100 AD, from Syria which at that time was influenced by Christianity, tells about the magoi, i.e. some Babylonian astronomers and astrologers, who by observing a certain star (later called “the Bethlehem Star”) by the mirroring water surface in a well in Northern Palestine, were able to calculate and find a certain local direction. None of these events would be understood by contemporaries, if this practice was not well known.

One of the most respected Greek scholars,  Eratosthenes (275-195 BC) calculated the circumference of the Earth by using the great well to observe the lack of shadows by the sun's meridian passage at summer solstice. This well from ancient pharaohnian times is placed the Elephantine Island in the Nile at Syene (Aswan) in Upper Egypt. The measuring of shadow angles was a very old method in Egypt.

http://www.ovs.thirax.dk/Artikel-X/Ove21/index-uk.htm

Pi - and the Papyrus Rhind

The application of geometrical calculations to the numbers in use by the astronomy implies a highly sophisticated stage of mathematic-geometrical skills by the ancient Egyptians. Indeed, this is confirmed by the mathematical (and geometrical) Papyrus Rhind, c. 1650 BC. Egyptian knowledge was famous - and at later times, Pythagoras coined his theorem of the right-angled triangle c. 550 BC, after having studied 22 years in Egypt. And Plato defined the Platonic solids c. 400 BC, after 13 years in Egypt, according to his pupil Eudoxus.

The concept of pi was known in Ancient Egypt. Much later, around 250 BC, Archimedes of Syracuse found that pi is somewhere about 3.14 (in fractions, Greeks did not have decimals). The digits of pi never end, nor has anyone detected an orderly pattern in their arrangement. Furthermore, pi is a transcendental number, i.e. a number which can't be expressed in any finite series of either arithmetical or algebraic operations. Pi transcends them. And pi is indescribable and unfitted to all rational methods to locate it.

 Moreover, a precise knownledge of pi was existing even before the pyramids more than 4,500 years ago. An important Egyptian measuring-unit is the cubit, which has an exact pi-relation to another Egyptian measuring-unit, the remen. Here, 1 remen constituates the radius of a cubit-square's circumscribed circle. Thus, these two standard mesuring-units were more easy and correct in use than calculating by fragments.

We don’t know to what extend this knowledge was conceived by the ancient Egyptians. When pi was applied to the more practical works all the conditions was not necessary to bring about. Earliest known Egyptian written reference to pi occurs in the afore-mentioned Papyrus Rhind, a scroll by the scribe Ahmesis of 15th Dynasty reign (Middle Kingdom era) of the Hyksos Pharaoh, Apepi I. (Found in Thebes/Luxor in the ruins of a small building near the Ramesseum).

The advanced levels of studies by the ancients were connected to the religious-mystical tradition, and the scroll’s opening words state about its own text that it is: “The Entrance Into the Knowledge of All Existing Things”. 
 

http://www.ovs.thirax.dk/Artikel-X/Ove21/index-uk.htm

http://www.ovs.thirax.dk/Artikel-X/Ove21/index-uk.htm

Recently, Dr. Eleanor Robson, an authority on Mesopotamian mathematics at the University of Cambridge, has made the case for a more mundane solution, arguing that the tablet was created as a teacher's aid, designed for generating problems involving right triangles and reciprocal pairs. Mr. Plimpton, who collected "our tools of learning" on a broad scale, would have been delighted with this interpretation, showing the work of an excellent teacher, not a lone genius a thousand years ahead of his time.

The Rhind Mathematical Papyrus (RMP) (also designated as: papyrus British Museum 10057, and pBM 10058), is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 B.C. The British Museum, where the papyrus is now kept, acquired it in 1864 along with the Egyptian Mathematical Leather Roll, also owned by Henry Rhind; there are a few small fragments held by the Brooklyn Museum in New York. It is one of the two well-known Mathematical Papyri along with the Moscow Mathematical Papyrus. The Rhind Papyrus is larger than the Moscow Mathematical Papyrus, while the latter is older than the former. [1]

The Rhind Mathematical Papyrus dates to the Second Intermediate Period of Egypt and is the best example of Egyptian mathematics. It was copied by the scribe Ahmes (i.e., Ahmose; Ahmes is an older transcription favoured by historians of mathematics), from a now-lost text from the reign of king Amenemhat III (12th dynasty). Written in the hieratic script, this Egyptian manuscript is 33 cm tall and over 5 meters long, and began to be transliterated and mathematically translated in the late 19th century. In 2008, the mathematical translation aspect is incomplete in several respects. The document is dated to Year 33 of the Hyksos king Apophis and also contains a separate later Year 11 on its verso likely from his successor, Khamudi.[2]

In the opening paragraphs of the papyrus, Ahmes presents the papyrus as giving “Accurate reckoning for inquiring into things, and the knowledge of all things, mysteries...all secrets”.

http://en.wikipedia.org/wiki/Moscow_and_Rhind_Mathematical_Papyri

(Actually, Moscow Papyrus is nearly 4000 years old. And Marshall Clagett translation is referenced where I'm using the image.)

The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenischev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Goleniš?ev. It later entered the collection of the Pushkin State Museum of Fine Arts in Moscow, where it remains today. Based on the palaeography of the hieratic text, it probably dates to the Eleventh dynasty of Egypt. Approximately 18 feet long and varying between 1 1/2 and 3 inches wide, its format was divided into 25 problems with solutions by the Soviet Orientalist Vasily Vasilievich Struve[1] in 1930.[2] It is one of the two well-known mathematical papyri along with the Rhind Mathematical Papyrus. The Moscow Mathematical Papyrus is older than the Rhind Mathematical Papyrus, while the latter is the larger of the two

http://en.wikipedia.org/wiki/Moscow_Mathematical_Papyrus